(Ciencias de Joseleg) (Química) (Química cuantitativa) (Estequiometría
analítica) (Ejercicios) (Introducción) (Historia) (Estequiometría
clásica) (Nueva
estequiometría) (Reactivo
limitante y reactivo en exceso) (Titulaciones
básicas) (Pureza,
rendimiento y eficiencia) (Las
gravimetrías) (Estequiometría
de gases) (Análisis
de composición) (Análisis
de cenizas) (Referencias
bibliográficas)
Tal como existieron dos teorías de la química, existen dos formas de hacer cálculos estequiométricos, pero en este caso, para la estequiometría clásica, la vencedora fue la basada en la noción de equivalencias estequiométricas. Esta estequiometría clásica es tan común que muchos piensan que es la única manera de hacer estos cálculos, sin embargo, en mi artículo “El Álgebra de la Estequiometría” (García-García, 2020) he demostrado que la interpretación matemática de equivalentes puede ser reemplazada por una interpretación atomista basada en álgebra, que es mucho más flexible, sin embargo para poder comparar entre las dos, veremos cómo se hacen los cálculos de masa por la estequiometría clásica.
El proceso de cálculo estequiométrico se basa en dos axiomas
básicos, la primera es que la ecuación estequiométrica de la reacción debe
encontrarse balanceada, la segunda es ignorar lo más posible la existencia de
átomos o moléculas, por lo que los coeficientes estequiométricos deberán ser
interpretados como cantidades de sustancia estándar, que han sido registrados
en experimentos anteriores y que son empleados en los cálculos con unidades de
cantidad de sustancia, o sea, moles.
La interpretación equivalentista puede hallarse en libros de
química modernos como Química La Ciencia Central (Brown et al., 2017. p103), donde se planea la relación
de equivalentes en moles para la siguiente ecuación química.
|
12. |
|
En el texto, definen a los coeficientes estequiométricos
como una cantidad relativa de moléculas involucradas en una reacción, sin
embargo, esta definición solo es cierta para la interpretación molar o
macroscópica de una reacción, en una interpretación molecular, los coeficientes
estequiométricos son cantidades absolutas, y por ende constantes que se
multiplican varias veces para dar las cantidades relativas.
De lo anterior entonces se indica que los coeficientes
estequiométricos se usan como cantidades de sustancia en moles y como
equivalentes, así la ecuación anterior se transforma en una visión
equivalentista de la siguiente manera:
|
13. |
|
Aunque el texto emplea un símbolo diferente de la igualdad, ya que la igualdad anterior violaría el principio matemático de identidad, las igualdades de las que hablamos aquí son proporciones:
|
14. |
|
Dicho símbolo significa "estequiométricamente
equivalente a". Relaciones estequiométricas como estas se
pueden usar para convertir cantidades de reactivos y productos en una reacción
química.
Adicionalmente debemos suponer que la reacción química es
completa, es decir, que consume todo el reactivo limitante hasta que se detiene
la reacción, aunque este presupuesto puede no cumplirse en casos especiales de
análisis de cenizas.
El último presupuesto descansa en el tipo de reacción por
reversibilidad, en este capítulo analizaremos la estequiometría de las
reacciones no reversibles, y en equilibrio el de las reacciones reversibles. De
esta manera, asumiremos que, para las reacciones no reversibles, la cantidad
inicial del producto es cero, y la cantidad final del reactivo limitante
también es cero.
Los casos estequiométricos se basan fundamentalmente en dos
grandes grupos, los cálculos de masas en donde no nos importa el reactivo
limitante, y aquellos en los que si nos importa. En los problemas en los que no
nos importa el reactivo limitante normalmente tenemos:
- Relaciones de cantidad de sustancia y masa.
- Relacione de unidades de concentración, sustancia y masa.
- Relacione de gases, unidades de concentración, sustancia y
masa.
- Eficiencia de la reacción.
- Reacciones incompletas.
- Análisis de combustión.
Para el caso de reactivo limitante, tendremos los primeros
tres, es decir:
- Relaciones de cantidad de sustancia y masa.
- Relacione de unidades de concentración, sustancia y masa.
- Relacione de gases, unidades de concentración, sustancia y
masa.
Algunos de estos casos pueden llegar a ser verdaderamente
retadores, y, por ende, en la enseñanza básica, empleando la técnica de
factores de conversión y cantidades de sustancia equivalentes, solo se logra
abarcar la primera de estas relaciones “Relaciones de cantidad de sustancia y
masa en situaciones donde no debemos tener en cuenta el reactivo limitante”.
En esta lección analizaremos estas situaciones que
constituyen la estequiometría clásica, por el método clásico de factores de
conversión, pero en las siguientes lecciones trabajaremos el método basado en
álgebra.
Las relaciones de cantidad de sustancia y masa en
situaciones donde no debemos tener en cuenta el reactivo limitante se pueden
dividir en cuatro casos concretos a saber: Mol a mol, Mol a gramo, Gramo a mol,
Gramo a Gramo. El método de factores de conversión es aritmético, y por ende no
generalizable en términos de fórmulas, sin embargo, los libros de texto han
propuesto diagramas de flujo para intentar reemplazar la función generalizadora
de una fórmula o ecuación matemática.
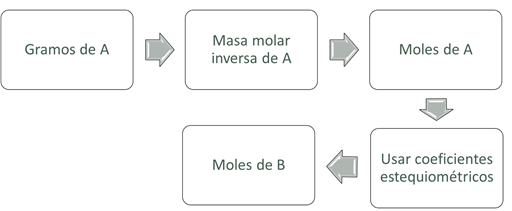
Figura 4. Diagrama de flujo para la
conversión de moles del dato (A) a moles de la incógnita (B).
El diagrama anterior nos indica que, la estequiometría se
interpreta aritméticamente como una conversión de unidades, empleando la
ecuación química balanceada como el patrón de equivalencia. Miremos un ejemplo
para ver cómo funciona:
Ejemplo
1. ¿Cuantos
moles de agua son producidos al reaccionar 8 moles de oxígeno gaseoso con
exceso de hidrógeno en la siguiente reacción?
Figura 5. Diagrama de flujo para la conversión de moles del dato
(A) a gramos de la incógnita (B).
En este caso la masa
molar deberá usarse en su forma invertida.
Ejemplo 2. ¿Cuántos gramos de agua se obtienen con 8 moles de oxígeno? YouTube
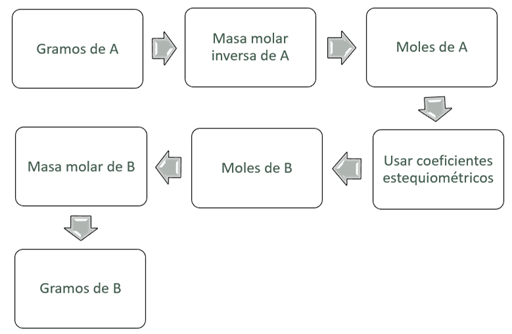
Figura 6. Diagrama de flujo para la conversión de gramos del dato
(A) a moles de la incógnita (B).
Ejemplo
3. De acuerdo a
la siguiente ecuación, cuantos moles de sulfato de potasio
Figura 7. Diagrama de flujo para la conversión de gramos del dato
(A) a gramos de la incógnita (B).
Ejemplo
4. De acuerdo a
la siguiente ecuación, ¿cuantos gramos de H2O2 se
requieren para consumir completamente 420 g H2SO4? 5H2O2+2KMnO4+3H2SO4
→K2SO4+2MnSO4+5O2+8H2O YouTube





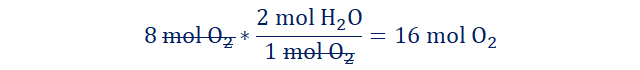



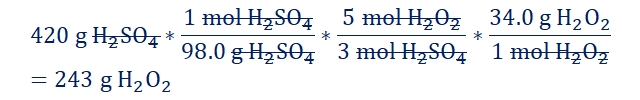

No hay comentarios:
Publicar un comentario