Química de Joseleg, cuantitativa: Modelo matemático de la solubilidad

(Ciencias de Joseleg) (Química) (Química cuantitativa) (Propiedades de las disoluciones) (Ejercicios) (Introducción) (Introducción a la solubilidad) (Electrolitos y conductividad) (Factores que afectan la solubilidad) (Solubilidad a nivel molecular) (Modelo matemático de la solubilidad) (La solución ideal y el factor de van't Hoff) (La ley de Henry) (Presión de vapor) (La ley de Raoult) (Diagramas de fase) (Aumento ebulloscópico y descenso crioscópico) (Propiedades coligativas de la atmósfera) (Ósmosis) (Coloides) (Referencias bibliográficas)

En las secciones anteriores hemos descrito cualitativamente como ocurre y por qué ocurre el proceso de solubilización. En esta sección nos enfocaremos en cuánto de un determinado soluto puede diluirse en una determinada cantidad de solvente bajo ciertas condiciones de temperatura. Nos enfocaremos principalmente en la solubilidad de solutos sólidos en el agua, mediante el instrumento denominado curva de Solubilidad.

Modelo general

La solubilidad puede modelarse como una verdadera ecuación química:

(4)

El equilibrio de la solubilidad representa el punto crítico en que una cantidad de solvente puede aguantar una cantidad de soluto acuoso, la reacción es reversible, y por ende esa cantidad cambia dependiendo de las condiciones del ambiente. Más allá de las consideraciones teóricas, la pregunta es ¿cómo resolvemos un problema de solubilidades? Y antes que esa, debemos plantearnos ¿en qué consiste un problema de equilibrio de solubilidades? Los problemas de equilibrio de solubilidades se pueden diferenciar en las siguientes acciones:

· Identificar la saturación del sistema.

· Identificar la masa máxima a las condiciones dadas.

· Identificar la masa faltante/sobrante.

De hecho, el modelo para resolver este problema será semejante al que emplearemos para los problemas de reactivo limitante en estequiometría. Para resolver esto, emplearemos la ecuación de avance de la reacción para un reactivo y para un producto, que es el modelo matemático general del equilibrio químico.

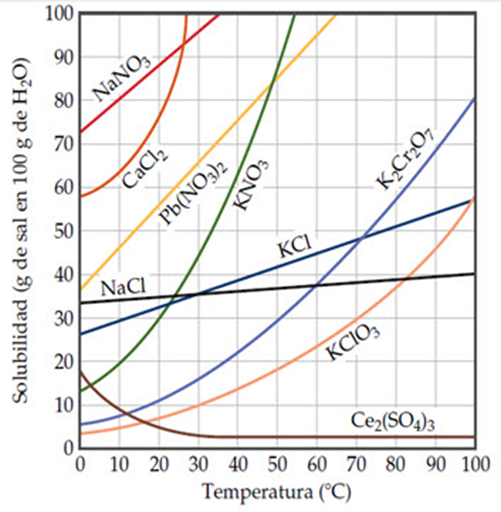
Figura 11. Curvas de solubilidad de varias sales, dependiendo de la temperatura a 100 g de solvente.

(5)

Demostración

En este caso asumiremos arbitrariamente que el reactivo es el sólido y el producto es el acuoso y que los coeficientes estequiométricos son iguales, al ser la misma sustancia.

La cantidad de sustancia acuosa inicial es cero ya que tendremos un solvente puro al inicio.

Dependiendo de la cantidad de sustancia sólida al final, determinaremos el índice de saturación de la solución, y por ende, despejaremos dicho termino.

Finalmente definimos la cantidad de sustancia acuosa, como la cantidad máxima que puede estar en estado acuoso.

(6)

Este es el modelo generalizado de la solubilidad, donde se dice que la cantidad de sustancia del cristalizado o precipitado n_i es la diferencia entre el agregado n_i⁰ y el que ha sido absorbido por el solvente y queda en estado acuoso n_aq. Sin embargo, la cantidad de sustancia que es absorbida en estado acuoso depende de la cantidad de solvente, y de aquí en más la de nominaremos cantidad máxima.

Convirtiendo a masas

Debido a que las tres sustancias en la ecuación (5) son de la misma sustancia, podemos reemplazar la cantidad de sustancia a masa sin ningún problema.

(7)

En este punto agregamos la notación T para indicar que la masa máxima y la masa del solido en equilibrio dependen de la temperatura del sistema.

Calculando la masa máxima

La masa máxima m_max es la masa final de una muestra tomada a partir de una solución estándar de concentración constante, esta concentración estándar es el límite crítico a una temperatura dada, y por ende se la denomina solubilidad y se le da su propio símbolo s_i,T, pero tenga en cuenta que este símbolo representa a una concentración.

El problema aquí es que s_i,T puede asumir cualquiera de las unidades de concentración vistas, pero la más usada en este contexto es una que no hemos visto, siendo masa de soluto entre masa de solvente:

(8)

Donde m^*_i,T es la masa de soluto que se encuentra en equilibrio de saturación con la cantidad estándar de solvente m_ii^* que generalmente son 100 g de agua. Estos valores estándar se dan como parte del texto de enunciado, en una tabla o en una gráfica.

Ahora, el punto es que la masa máxima dependiente de la temperatura m_max,T que puede absorber un solvente m_ii está diluida en una cantidad final de solvente que se relaciona con la misma solubilidad de la solución estándar dependiente de la temperatura s_i,T.

Por lo que podemos igualar ambas expresiones:

(9)

(10)

Y por lo anterior, podemos calcular la masa máxima que puede absorber una cantidad arbitraria de solvente por medio de los valores estándar a una temperatura determinada.

(11)

La ecuación final

Con la definición de la masa máxima podemos reemplazar en (7).

(12)

A 500 g de agua se le añaden se le añaden 35 g de CaCl₂ a una temparatura de 70°C. ¿Cómo es la disolución obtenida? ¿Qué ocurre si enfriamos la disolución a 30 °C? Obtenga resultados numéricos. La solubilidad crítica a 70°C es de 6 g en cada 100 g de solvente; y a 30°C es de 8 g en 100 g de solvente.

Solución analítica: Aplicamos la ecuación (12).

Solución numérica

A 70 °C.

Como tenemos una masa de soluto sólido final de 5 g, la solución se encuentra sobresaturada.

A 30 °C.

Como la masa de soluto sólido final es de -5 g, esto implica que la solución está insaturada y faltan 5 g para saturarla.

En caso de que el solvente esté dado en volumen, podemos aproximar la respuesta asumiendo que la densidad de la solución es igual a la densidad del agua, y por ende convertir directamente ml a g.

La solubilidad del nitrato de plata, a 18 °C, es de 211,6 g en 100 mL de agua.

a) ¿Cuántos gramos de nitrato de plata se pueden disolver como máximo en 400 mL de agua a 18 °C?

b) ¿Cuánto nitrato hay que añadir a 1 L de agua para que se sature?

Solución analítica:

La solución del punto (a) se obtiene con la ecuación (11).

Para la solución (b) aplicamos la ecuación (12)., igualando la masa sólida a 0, que es la condición de saturación.

Solución numérica: aproximamos la respuesta asumiendo 100ml=100gL 400 mL=400g; y 1 L = 1000 g.

Punto (a)

Punto (b), convierta

La solubilidad del nitrato de potasio, a 30°C, es de 40 g en 100 g de agua. ¿Cuánta masa de nitrato quedará sin disolver en un vaso con 300 mL de agua si añadimos, agitando, 170 g de nitrato a 30 °C?

Solución analítica: Aplicamos la ecuación (12).

Solución numérica: Tenga en cuenta que el solvente estándar está en gramos y el solvente usado está en mililitros, convertiremos implícitamente el volumen a masa, dado que la densidad del agua es 1g/mol, solo es expresar 300 g en lugar de 300 ml.