(Ciencias de Joseleg) (Química) (Química cuantitativa) (Disoluciones
y propiedades coligativas) (Ejercicios) (Introducción) (Generalidades) (Mezclas
homogéneas y heterogéneas) (Mezclas
homogéneas o disoluciones) (Tipos
de disoluciones) (Introducción
a las unidades de concentración) (Porcentaje
en masa) (Notación
partes por) (Porcentaje
volumen a volumen) (Porcentaje
masa a volumen) (Concentración
molar) (Concentración
normal) (Peso
equivalente y factor equivalente) (Concentración
molal) (Fracción
molar) (Conversiones
entre unidades de concentración líquidas)
(Unidades
de concentración en gases) (Conversiones
de unidades de concentración gaseosas)
(Cambios
de concentración subcríticos) (Alícuotas,
destilaciones y mezclas) (Referencias
bibliográficas)
Aparte del número de equivalentes y el equivalente molar, históricamente, la concentración equivalente o concentración normal has estado vinculada a otras magnitudes físicas. Las más notables son el factor equivalente y el peso equivalente.
El factor
equivalente se define como el inverso del equivalente molar, es decir, los
moles de sustancia por cada equivalente en carga.
(64)
Como tal, puede ser
calculado con la misma información de un equivalente molar, solo que,
invirtiendo los datos, o sacando el inverso del equivalente molar.
(65)
Adicionalmente, el
factor equivalente generalmente es sinónimo de peso equivalente en fuentes como
la tabla 10-6 de la química de Matamala y Gonzalez (1976), pero eso no es
necesariamente cierto, pues el factor equivalente se define con moles y no con
gramos. Sin embargo, al convertir cantidad de sustancia a masa sí obtendremos el
peso equivalente.
El peso equivalente gramo “masa equivalente en nuestra
terminología moderna” Ew fue un concepto creado antes de la definición
de las masas molares, y dicho concepto estaba imbuido en él. Tal como se
define, el peso equivalente gramo tiene unidades de g/eq, por lo que podemos
demostrar sus unidades del siguiente modo.
Demostración
Multiplicamos la definición del
factor equivalente por la masa molar
Cancelamos cantidades de
sustancia
Las unidades resultantes son masa sobre número de equivalentes (g/eq). De lo anterior, podemos definir al peso equivalente-gramo como el producto de la masa molar y el factor equivalente.
(66)
(67)
(68)
El libro dorado de la IUPAC no tiene un símbolo
estandarizado para esta variable. De esta manera podemos calcular
deductivamente el peso equivalente gramo a partir de la masa molar y el
equivalente molar.
Los primeros pesos equivalentes fueron publicados para
ácidos y bases por Carl Friedrich Wenzel (Wenzel,
1777). Jeremias Benjamin Richter preparó
un conjunto más grande de tablas, posiblemente de forma independiente, a partir
de 1792 (Richter,
1792). Sin
embargo, ni Wenzel ni Richter había un solo punto de referencia para sus
tablas, por lo que tuvieron que publicar tablas separadas para cada par de
ácido y base.
La primera tabla de pesos atómicos de John Dalton (1808)
sugirió un punto de referencia, al menos para los elementos: tomar el peso
equivalente de hidrógeno como una unidad de masa (Dalton,
2010). Sin
embargo, la teoría atómica de Dalton estaba lejos de ser universalmente
aceptada a principios del siglo XIX. Uno de los mayores problemas fue la
reacción del hidrógeno con el oxígeno para producir agua.
Un gramo de hidrógeno reacciona con ocho gramos de oxígeno
para producir nueve gramos de agua (Ver La
teoría atómica de Dalton), por lo que el peso equivalente de oxígeno se
definió como ocho gramos. Como Dalton suponía (incorrectamente) que una
molécula de agua consistía en un átomo de hidrógeno y un átomo de oxígeno, esto
implicaría un peso atómico de oxígeno igual a ocho. Sin embargo, expresando la
reacción en términos de volúmenes de gas siguiendo la ley de Gay-Lussac de
combinar volúmenes de gas, dos volúmenes de hidrógeno reaccionan con un volumen
de oxígeno para producir dos volúmenes de agua, lo que sugiere (correctamente)
que el peso atómico del oxígeno es dieciséis.
El trabajo de Charles Frédéric Gerhardt (1816-1856), Henri Victor
Regnault (1810-1878) y Stanislao Cannizzaro (1826-1910) ayudó a racionalizar esta
y muchas paradojas similares, pero el problema seguía siendo el tema de debate
en el Congreso de Karlsruhe (Wurtz, 1860).
Sin
embargo, todas las magnitudes equivalentes que hemos establecido hasta este
momento están vinculadas a la sustancia, mientras que los pesos equivalentes
históricos están vinculados a los elementos. Para obtener las magnitudes
equivalentes de los elementos, deberemos emplear el estado de oxidación de cada
elemento en lugar de la carga real del ion.
(69)
Que tenemos
el equivalente molar del elemento podemos reemplazar en la ecuación de peso
equivalente.
(70)
La forma convidada de ambas
(71)
Donde emu es igual a 1 eq/mol. A pesar de que ya estamos cerca, estos valores aún no son los pesos equivalentes históricos, pues los pesos equivalentes históricos estaban dados en valores a dimensionales o relativos al hidrógeno. Por ende, podemos concluir que el peso equivalente histórico es el radio de pesos equivalentes, donde el denominador siempre es hidrógeno.
Ejemplo. Determine
el peso equivalente del hidrógeno y el oxígeno en el agua.
Solución analítica:
Análisis químico.
En el agua el estado de oxidación del hidrógeno es +1 y el estado de
oxidación del oxígeno es -2.
Para obtener los pesos equivalentes
históricos sólo es dividir todos los valores entre el peso equivalente del
hidrógeno, Con lo que el peso equivalente relativo del hidrógeno es 1, y el peso equivalente del oxígeno 7.92, a 8.
Sin embargo, muchos
químicos encontraron que los pesos equivalentes son una herramienta útil sin
tener que contar con las hipótesis atómicas, que en su época eran muchas. Los
pesos equivalentes fueron una generalización útil de la ley de proporciones
definidas de Joseph Proust (1794) que permitió que la química se convirtiera en
una ciencia cuantitativa. El químico francés Jean-Baptiste Dumas (1800–84) se
convirtió en uno de los oponentes más influyentes de la teoría atómica, después
de haberla abrazado anteriormente en su carrera, pero era un firme defensor de
pesos equivalentes.
Los pesos
equivalentes no estaban exentos de problemas propios. Para empezar, la escala
basada en hidrógeno no era particularmente práctica, ya que la mayoría de los
elementos no reaccionan directamente con el hidrógeno para formar compuestos
simples. Sin embargo, un gramo de hidrógeno reacciona con 8 gramos de oxígeno
para dar agua o con 35.5 gramos de cloro para dar cloruro de hidrógeno: por lo
tanto, 8 gramos de oxígeno y 35.5 gramos de cloro pueden considerarse
equivalentes a un gramo de hidrógeno para la medición de pesos equivalentes.
Este sistema puede extenderse aún más a través de diferentes ácidos y bases (Administration
du grand dictionnaire universel, 1866).
Mucho más grave fue
el problema de los elementos que forman más de un óxido o serie de sales, que
tienen (en la terminología actual) diferentes estados de oxidación. El cobre
reaccionará con el oxígeno para formar óxido cuproso rojo ladrillo (óxido de
cobre (I), con 63,5 g de cobre por 8 g de oxígeno) u óxido cúprico negro (óxido
de cobre (II), con 31,7 g de cobre por 8 g de oxígeno)
Por lo que tiene
dos pesos equivalentes. Los partidarios de los pesos atómicos podrían recurrir
a la ley Dulong-Petit (1819), que relaciona el peso atómico de un elemento
sólido con su capacidad calorífica específica, para llegar a un conjunto único
y sin ambigüedades de pesos atómicos (Administration
du grand dictionnaire universel, 1866). La
mayoría de los partidarios de los pesos equivalentes, que eran la gran mayoría
de los químicos antes de 1860, simplemente ignoraron el hecho inconveniente de
que la mayoría de los elementos exhibían múltiples pesos equivalentes. En
cambio, estos químicos se habían establecido en una lista de lo que
universalmente se llamaban "equivalentes" (H = 1, O = 8, C = 6, S =
16, Cl = 35.5, Na = 23, Ca = 20, y así sucesivamente).
Sin embargo, estos
"equivalentes" del siglo XIX no eran equivalentes en el sentido
original o moderno del término. Como representaban números adimensionales que
para cualquier elemento dado eran únicos e inmutables, en realidad eran
simplemente un conjunto alternativo de pesos atómicos, en el que los elementos
de valencia uniforme tienen pesos atómicos la mitad de los valores modernos.
Este hecho no fue reconocido hasta mucho más tarde (Rocke, 1984).
El golpe final de
muerte para el uso de pesos equivalentes para los elementos fue la presentación
de Dmitri Mendeleev de su tabla periódica en 1869, en la que relacionó las
propiedades químicas de los elementos con el orden aproximado de sus pesos
atómicos. Sin embargo, se siguieron utilizando pesos equivalentes para muchos
compuestos durante otros cien años, particularmente en química analítica. Los
pesos equivalentes de los reactivos comunes podrían tabularse, simplificando
los cálculos analíticos en los días previos a la disponibilidad generalizada de
calculadoras electrónicas: tales tablas eran comunes en los libros de texto de
química analítica.
Históricamente, los
pesos equivalentes de los elementos a menudo se determinaron estudiando sus
reacciones con el oxígeno, el cual tendría el estandar de 8 g/eq. Por ejemplo,
50 g de zinc reaccionarán con el oxígeno para producir 62,24 g de óxido de
zinc, lo que implica que el zinc ha reaccionado con 12,24 g de oxígeno (de la
Ley de conservación de la masa): el peso equivalente de zinc es la masa que
reaccionar con ocho gramos de oxígeno, por lo tanto 50 g × 8 g / 12,24 g = 32,7
g.
El uso de pesos
equivalentes en química general ha sido reemplazado en gran medida por el uso
de masas molares, aunque estos términos se encuentran vinculados, y como hemos
visto, es posible obtener los históricos pesos equivalentes por medio de los
equivalentes molares (o factores equivalentes) y las masas molares.
El factor equivalente y el peso equivalente son magnitudes históricas
que se usan rara vez en la química moderna. Sin embargo, el problema radica en
que la mayoría de las definiciones de la concentración normal para uso práctico
convocan estas dos magnitudes. Así que procederemos a demostrar por qué
funcionan estas otras definiciones de la concentración equivalente o
concentración normal.
Demostración
Iniciamos con la definición de concentración
equivalente en términos del equivalente molar que vimos en la sección anterior.
Y la definición de factor equivalente en
términos del equivalente molar.
Al igualar ambas expresiones por medio del
equivalente molar, obtenemos el cálculo de la concentración equivalente en
términos del factor equivalente, que es como definen concentración normal en la
Wikipedia.
(72)
Demostración
Para definir la concentración equivalente en
términos del peso equivalente, vamos a tomar la ecuación anterior y la
definición de peso equivalente en términos del factor equivalente.
Igualamos
ambas expresiones por medio del factor equivalente.
Finalmente,
multiplicar cantidad de sustancia por la masa molar nos da la masa del soluto.
(73)


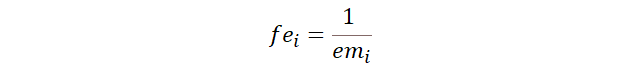

















No hay comentarios:
Publicar un comentario