(Ciencias de Joseleg) (Química) (Química cuantitativa) (Propiedades
de las disoluciones) (Ejercicios) (Introducción) (Introducción
a la solubilidad) (Electrolitos
y conductividad) (Factores
que afectan la solubilidad) (Solubilidad
a nivel molecular) (Modelo
matemático de la solubilidad) (La
solución ideal y el factor de van't Hoff)
(La
ley de Henry) (Presión
de vapor) (La
ley de Raoult) (Diagramas
de fase) (Aumento
ebulloscópico y descenso crioscópico)
(Propiedades
coligativas de la atmósfera) (Ósmosis) (Coloides) (Referencias
bibliográficas)
Las propiedades coligativas de las soluciones son
propiedades que dependen de la concentración de iones o moléculas de soluto,
pero no de la identidad del soluto. Aunque esta es la definición clásica, la
verdad es que la identidad del soluto muchas veces influye en la cantidad de
iones liberados en una solución, ya sea porque al disociarse libera más
equivalentes por cada mol que otros, o porque ingresa en equilibrio químico y
por ende las cantidades liberadas literalmente dependen de su identidad. Por lo
anterior, hay que destacar que, aunque se nos diga que la identidad química de
la sustancia es un aspecto secundario, cuando creemos los modelos matemáticos
veremos que si es importante.
La relación numérica entre el número de partículas de soluto
con respecto al solvente o a la solución puede estar relacionada con las
diversas unidades de concentración de una solución, por ejemplo, molaridad,
molalidad, normalidad etc. La suposición de que las propiedades de la solución
son independientes de la naturaleza de las partículas de soluto es exacta solo
para soluciones ideales, y es aproximado para soluciones reales diluidas. En
otras palabras, las propiedades coligativas son un conjunto de propiedades de
la solución que pueden aproximarse razonablemente suponiendo que la solución es
ideal.
Para una relación de masa soluto-disolvente dada, todas las
propiedades coligativas son inversamente proporcionales a la masa molar del
soluto.
La medición de propiedades coligativas para una solución
diluida de un soluto no ionizado como urea o glucosa en agua u otro solvente
puede conducir a determinaciones de masas molares relativas, tanto para
moléculas pequeñas como para polímeros que no pueden estudiarse por otros
medios. Alternativamente, las mediciones de solutos ionizados pueden llevar a
una estimación del porcentaje de disociación que tiene lugar.
Las propiedades coligativas se estudian principalmente para
soluciones diluidas, cuyo comportamiento puede aproximarse al de una solución
ideal.
En química, una solución ideal o mezcla ideal es una
solución en la que la fase gaseosa exhibe propiedades termodinámicas análogas a
las de una mezcla de gases ideales (Felder, Rousseau, & Bullard, 2020). La entalpía de la mezcla es
cero al igual que el cambio de volumen al mezclar por definición; cuanto más
cercana a cero es la entalpía de mezcla, más "ideal" se vuelve el
comportamiento de la solución. La presión de vapor de la solución obedece a la
ley de Raoult o la ley de Henry (o ambas), y el coeficiente de actividad de
cada componente (que mide la desviación de la idealidad) es igual a uno.
El concepto de solución ideal es fundamental para la
termodinámica química y sus aplicaciones, como el uso de propiedades
coligativas. La idealidad de las soluciones es análoga a la idealidad para los
gases, con la importante diferencia de que las interacciones intermoleculares
en los líquidos son fuertes y no pueden simplemente descuidarse como ocurre con
los gases ideales. En cambio, asumimos que la fuerza media de las interacciones
es la misma entre todas las moléculas de la solución “lo cual justifica la
aplicación de modelos lineales”.
Si las moléculas de una solución son químicamente casi
idénticas, por ejemplo, 1-butanol y 2-butanol, entonces la solución será casi
ideal. Dado que las energías de interacción entre A y B son casi iguales, se
deduce que hay un cambio de energía total (entalpía) muy pequeño cuando se
mezclan las sustancias. Cuanto más diferente sea la naturaleza de A y B, más se
espera que la solución se desvíe de la idealidad. Loanterior también se cumple
si hay una poca cantidad de una sustancia diluida en otra, y por ende, las
soluciones ideales son aquellas que se encontrarán a muy bajas concentraciones.
Las desviaciones de la idealidad se pueden describir
mediante el uso de funciones de Margules o coeficientes de actividad. Un solo
parámetro de Margules puede ser suficiente para describir las propiedades de la
solución si las desviaciones de la idealidad son modestas; tales soluciones se
denominan regulares. A diferencia de las soluciones ideales, donde los
volúmenes son estrictamente aditivos y la mezcla siempre es completa, el
volumen de una solución no ideal no es, en general, la simple suma de los
volúmenes de los componentes líquidos puros y la solubilidad no está
garantizada en el conjunto. rango de composición. Mediante la medición de
densidades se puede determinar la actividad termodinámica de los componentes.
Aun cuando asumimos que una solución es ideal, aún nos queda
el problema de la ionización y el número de partículas. El factor de van 't
Hoff “ii” (llamado así por el
químico holandés Jacobus Henricus van' t Hoff) es una medida del efecto de la
ionización de un soluto sobre las propiedades coligativas.
El factor de van't Hoff es la relación entre la
concentración real de partículas producidas cuando la sustancia se disuelve y
la concentración de una sustancia calculada a partir de su masa. Para la
mayoría de los no electrolitos disueltos en agua, el factor van't Hoff es
esencialmente 1.
Para la mayoría de los compuestos iónicos disueltos en agua,
el factor van't Hoff es igual al número de iones discretos en una unidad de
fórmula de la sustancia. Esto es cierto solo para las soluciones ideales, ya
que ocasionalmente se produce un apareamiento de iones en la solución. En un
instante dado, un pequeño porcentaje de los iones se emparejan y cuentan como
una sola partícula. El apareamiento de iones ocurre hasta cierto punto en todas
las soluciones de electrolitos. Esto hace que el factor de van't Hoff medido
sea menor que el predicho en una solución ideal. La desviación del factor de
van't Hoff tiende a ser mayor cuando los iones tienen cargas múltiples.
La buena noticia es que normalmente asumiremos factores de
van't Hoff ideales, normalmente perteneciendo a no electrolitos. Por lo tanto,
calcularemos el factor de van't Hoff como la suma de los coeficientes
estequiométricos de los iones reactivos de un electrolito fuerte.
(13)
Por ejemplo, i = 2
para NaCl en agua, asumiendo una disociación completa de iones. Como resultado,
esperamos que la elevación del punto de ebullición de una solución acuosa de
NaCl de 1 molal sea dos veces más grande que la elevación del punto de
ebullición de una solución de 1 molal de un no electrolito como la sacarosa.
Por lo tanto, para predecir correctamente el efecto de un soluto en particular
en la elevación del punto de ebullición (o cualquier otra propiedad
coligativa), es importante saber si el soluto es un electrolito o un no
electrolito.
Las propiedades coligativas de las soluciones dependen de la
concentración total de partículas de soluto, independientemente de si las
partículas son iones o moléculas. Por lo tanto, esperamos que una solución de
NaCl de 0,100 molal tenga una depresión del punto de congelación de (2)(0.100
m)(1.86 ° C/m) = 0,372 °C debido a que tomamos i = 2. Sin embargo, la depresión medida del punto de congelación es
de solo 0,348 °C y la situación es similar para otros electrolitos fuertes. Una
solución de 0,100 m de KCl, por ejemplo, se congela a —0.344 ° C.
La diferencia entre las propiedades coligativas esperadas y
observadas para electrolitos fuertes se debe a las atracciones electrostáticas
entre iones. A medida que los iones se mueven en solución, los iones de carga
opuesta chocan y se “pegan” durante breves instantes. Mientras están juntos, se
comportan como una sola partícula llamada par de iones (Figura
12).
De este modo se reduce el número de
partículas independientes, lo que provoca una reducción en la depresión del
punto de congelación (así como en la elevación del punto de ebullición,
reducción de la presión de vapor y presión osmótica).
Hemos supuesto que el factor de van't Hoff, es igual a la
suma de coeficientes estequiométricos de un electrolito fuerte “ecuación (13)”.
Sin embargo, el valor real (medido) de este factor viene dado por la relación
entre el valor medido de una propiedad coligativa y el valor calculado cuando
se supone que la sustancia no es un electrolito. Usando la depresión del punto
de congelación, por ejemplo, tenemos:
(14)
Figura 12. Apareamiento de iones y propiedades coligativas. Una solución de NaCl contiene no solo iones de Na+(aq) y Cl—(aq) separados, sino también pares de iones.
En ausencia de información sobre el valor real de i para una solución, usaremos el valor de la
ecuación (13).
Los valores reales se encuentran consignados en tablas como las siguientes.
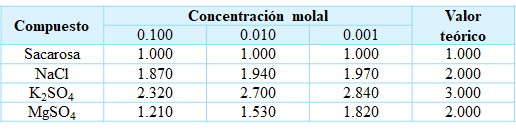
Tabla 2. Valores experimentales y teóricos
del factor de van't Hoff para varias sustancias a 25°C.
En la Tabla 2.,
se observan dos tendencias, que muestran los factores de van’t Hoff medidos
para varias sustancias en diferentes diluciones. Primero, la dilución afecta el
valor de i
para los electrolitos; cuanto más diluida la solución, más se acerca i al
valor esperado basado en el número de iones en la unidad de fórmula. Por tanto,
llegamos a la conclusión de que el grado de apareamiento de iones en las
soluciones de electrolitos disminuye con la dilución, o lo que es lo mismo, una
solución se comportará más idealmente mientras más diluida se encuentre. En
segundo lugar, cuanto más bajas son las cargas de los iones, menos se aleja i del
valor esperado porque la extensión del apareamiento de iones disminuye a medida
que disminuyen las cargas iónicas. Ambas tendencias son consistentes con la
electrostática simple: la fuerza de interacción entre partículas cargadas
disminuye a medida que aumenta su separación y disminuyen sus cargas.
Las propiedades coligativas incluyen disminución de la presión de vapor, elevación del punto de ebullición, depresión del punto de congelación y presión osmótica. Sin embargo, estas las veremos más adelante de manera más detallada.





No hay comentarios:
Publicar un comentario