(Ciencias de Joseleg) (Química) (Química cuantitativa) (Estequiometría
analítica) (Ejercicios) (Introducción) (Historia) (Estequiometría
clásica) (Nueva
estequiometría) (Reactivo
limitante y reactivo en exceso) (Titulaciones
básicas) (Pureza,
rendimiento y eficiencia) (Las
gravimetrías) (Estequiometría
de gases) (Análisis
de composición) (Análisis
de cenizas) (Referencias
bibliográficas)
Hasta ahora en los ejercicios de lápiz y papel, el enunciado nos identificaba el reactivo limitante en caso de calcular una sustancia producto, o nos preguntaban la cantidad de un reactivo para establecer una mezcla en la que no hay sobrantes ni faltantes, pero este tipo de mezclas ideales no son siempre reales, ¿Qué pasa cuando una mezcla estequiométrica de reactivos no es ideal?
Cuando no hay suficiente de un reactivo en una reacción química, la reacción se detiene abruptamente, en este caso tenemos una mezcla no ideal de reactivos. El reactivo que detiene la reacción al extinguirse completamente se denomina el reactivo limitante, y el que queda sin encontrar más con quien reaccionar es el reactivo en exceso.
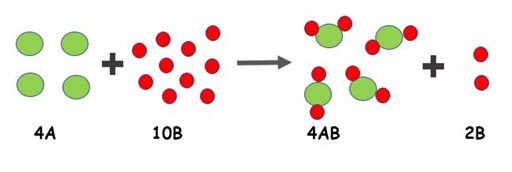
Figura 8. Reacción química con reactivo limitante y en exceso
En la
figura anterior se muestra una relación de síntesis de dos sustancias, A y B,
para sintetizar AB2, sin embargo, debido a que hay muchas partículas
de B, estas quedan sobrando ya que no hay suficiente A.
Para calcular la cantidad de producto producido, se debe
determinar el reactivo que limitará la reacción química (el reactivo limitante)
y qué reactivo está en exceso (el reactivo en exceso). Existen dos variables a
tener en cuenta para identificar el reactivo limitante:
- coeficiente estequiométrico elevado.
- cantidad de sustancia baja.
Los reactivos con coeficientes estequiométricos elevados se
consumen más rápido por ciclo de reacción que aquellos con coeficientes
estequiométricos cercanos a 1. Y aquella sustancia con menor cantidad de
partículas absoluta pues tenderá a ser limitante. No existe una variable más
importante que otra, por ejemplo, aunque una sustancia tenga un gran
coeficiente estequiométrico que condiciona su rápida desaparición, si agregamos
moles en exceso, esta será el reactivo en exceso.
Sin embargo, a veces analizar cualitativamente estas
situaciones conlleva a errores, por lo que se plantean soluciones
cuantitativas.
Una forma de encontrar el reactivo limitante es calculando
la cantidad de producto que puede formar cada reactivo; el que produce menos producto
es el reactivo limitante, a esta estrategia la denominaremos estrategia
aritmética clásica.
Sin embargo, ¿sería posible plantear una solución analítica
universal para este tipo de situaciones?
Es una pregunta retórica porque la respuesta es sí, y en mi artículo
(García-García 2020) planteo la solución a partir de la ecuación de avance de
la reacción.
Recuerde que la deducción solo la hago para justificar la
validez de las ecuaciones de trabajo finales, que serán solo dos, uno para
identificar quien es el reactivo limitante por medio del factor Rl, y
otra para hallar la cantidad de sustancia o masa del relativo sobrante o
faltante.
Deducción
Emplearemos la ecuación de avance
de la reacción, pero únicamente para una pareja de reactivos A y B.
Descomponemos la suma, para que
cada cantidad de sustancia tenga su coeficiente estequiométrico.
Despejamos el momento inicial a
la izquierda y el momento final a la derecha.
Por esta ruta, que es más rápida, obtenemos una definición
más general del factor de identificación (Rl).
Pues no solo involucra las cantidades iniciales, sino también las cantidades
finales. En general emplearemos la expresión para momento inicial (18)
para identificar quien es el reactivo límite, pero en términos prácticos es
conveniente manejarla de la siguiente manera.
22.
Las marcas superiores nos ayudarán a relacionar el signo de
Rl con la sustancia, si Rl es positivo entonces A está en exceso, y su Rl es
negativo entonces B está en exceso.
La expresión para cantidades finales, que omitimos al
calcular Rl, tiene una utilidad, y es el cálculo de cantidades faltantes y
sobrantes.
Deducción
Asumamos que la sustancia A es
el reactivo limitante, si eso es cierto su cociente al finalizar (nA/vA)
vale cero. Por lo que podemos tomar la ecuación 21., y simplificarla
Despejamos la cantidad de
sustancia de B.
Lo interesante es que la
ecuación anterior funciona no solo para B, sino para cualquiera sustancia, y
para cualquier situación, sea los moles faltantes o sobrantes, por lo que la
generalizaremos a:
23.
En otras palabras, solo es multiplicar el valor absoluto de Rl
por el coeficiente estequiométrico del sobrante o el faltante. Si se
necesita la masa, solo es reemplazar cantidad de sustancia por el cociente masa
sobre masa molar.
Ejemplo
10. Ponemos a reacción 20 mol de hidrógeno con 20 mol de
oxígeno, identifique el reactivo limitante, y cuanto del reactivo sobrante
queda sin reaccionar. 2H2(g)+O2(g)→2H2O(g). YouTube.
Como
el resultado es negativo se concluye que el reactivo limitante es el hidrógeno
y el relativo en exceso es el oxígeno.
Ejemplo
11. Si reaccionan 124 g de P4 (124 g/mol) con 210
g de Cl2 (70 g/mol), ¿identifique la masa sobrante de fósforo? P4+6Cl2→4PCl3 YouTube.
Como ambas sustancias estan dadas en masa, reemplazamos
(n) por (m/M) en la ecuación de Rl.
Y lo mismo con la ecuación para calcular sobrantes o
faltantes.
Ahora solo es combinarlas y reemplazar valores, pues ya
sabemos por el enunciado que la sustancia sobrante es el fósforo.
Ejemplo 12. Al inicio se ponen a reaccionar 4,5 g de MnO2 con 4,0 g de HCl. ¿Cuántos gramos de Cl2 se obtienen? Calcular la cantidad de reactivo en exceso que queda sin reaccionar. MnO2(s)+4HCl(ac)→MnCl2(ac)+Cl2(g)+2H2O(l). Cl=35; H=1; O=16; Mn=55 YouTube.
Calculamos las masas
molares de las sustancias involucradas.
Este ejercicio combinado nos hace las preguntas en orden contrario al cálculo, lo primero es identificar el reactivo en exceso con:
Como el valor de Rl es positivo,
el reactivo en exceso es MnO2 y haremos la estequiometría gramo a
gramo con el reactivo limitante.
Y para hallar la masa sobrante
tomaremos la ecuación: