(Ciencias de Joseleg) (Química) (Química cuantitativa) (Disoluciones
y propiedades coligativas) (Ejercicios) (Introducción) (Generalidades) (Mezclas
homogéneas y heterogéneas) (Mezclas
homogéneas o disoluciones) (Tipos
de disoluciones) (Introducción
a las unidades de concentración) (Porcentaje
en masa) (Notación
partes por) (Porcentaje
volumen a volumen) (Porcentaje
masa a volumen) (Concentración
molar) (Concentración
normal) (Peso
equivalente y factor equivalente) (Concentración
molal) (Fracción
molar) (Conversiones
entre unidades de concentración líquidas)
(Unidades
de concentración en gases) (Conversiones
de unidades de concentración gaseosas)
(Cambios
de concentración subcríticos) (Alícuotas,
destilaciones y mezclas) (Referencias
bibliográficas)
Las ecuaciones o modelos matemáticos se diseñan para ciertas situaciones o presupuestos, por ejemplo, las ecuaciones de (96) a (137) presuponen una disolución líquida, sin embargo, si cambiamos la naturaleza del sistema también cambia el modelo matemático.
Para modelar gases, las relaciones de varias unidades de
concentración se modifican con respecto a sus versiones en disoluciones
líquidas, la clave para encontrar las relaciones (que no serán todas), radicará
en la ley de los gases ideales.
(138)
La ecuación anterior se encuentra definida para un gas
soluto cualquiera, pero debido a la idealidad de los gases ideales y los presupuestos
de las leyes de Dalton, la ecuación también es válida para la totalidad de
gases en una mezcla.
(139)
Cuando analizamos las propiedades de los gases vimos una
manera de determinar la concentración de un gas, siendo esta la concentración
molar, sin embargo, existen otras formas de expresar la concentración de un gas
en una mezcla de gases, dos de ellas particularmente importantes, derivables de
la ley de los gases ideales. Si dividimos la ecuación estática para la forma
dinámica, pero no para un cambio sino para una dispersión, donde los términos
del numerador son de uno de los gases componentes que llamaremos solito (i) y el otro la mezcla total (sin subíndice) obtendremos lo siguiente.
(140)
Si asumimos que la presión total y la temperatura total son
iguales a las que tiene el gas soluto obtendremos la siguiente igualdad.
(141)
En ambos casos tenemos una medida de la dispersión, siendo
la primera conocida como fracción de volúmenes, siendo generalmente expresada en
una forma porcentual:
(142)
Y la segunda forma se conoce como fracción molar.
(143)
Una propiedad a tener en cuenta de las fracciones, ya sea de
disoluciones líquidas o de gases es que el total de cualquier fracción,
expresada como la suma de fracciones parciales será igual a 1.
Sin embargo, las fracciones no son las únicas variables
totales que pueden expresarse como la suma de variables parciales, algunas
otras son:
Los gases no se ionizan, y cuando lo hacen pasan a ser
plasma, y la concentración molal total no estaría definida.
Las unidades de
concentración básicas de los gases se obtienen al dividir la ley de los gases
ideales del gas soluto entre la ley de los gases ideales de la suma de gases, y
asumimos temperatura constante debido a que el gas soluto debe estar en
equilibrio térmico con los demás gases de la mezcla.
(156)
Si asumimos un
recipiente rígido de presión constante, tendremos lo siguiente.
(157)
Estos cocientes
definen dos unidades de concentración, la fracción de volumen y la fracción
molar, por ende, en gases, la identidad fundamental de conversión de unidades
de concentración dicta que la fracción de volumen es equivalente a la fracción
molar:
(158)
Para hallar la masa molar total retomaremos desde la forma
dinámica de los gases ideales, pero empleando masas en lugar de cantidad de
sustancia:
Demostración
Al cancelar las constantes
obtenemos lo siguiente:
El cociente masa sobre la masa
total se conoce como la fracción de masas:
Y, por ende, recuperamos la
fracción de volumen, que es igual a la fracción molar a la izquierda, y la
fracción de masas a la derecha.
La pregunta sería ¿Cómo calcular
la masa molar total, sin contar con la fracción de masas? Omitiremos la
fracción de volúmenes y despejaremos la fracción de masas.
Ahora sumamos todas las
variables:
Reemplazamos la suma de fracción
de masas por y sacamos factor común en el otro lado de la expresión:
Y finalmente despejamos la masa
molar de la mezcla:
(159)
A continuación, veremos cómo esta batería de ecuaciones es
empleada para describir la mezcla de gases más universalmente distribuida, el
aire.
Con frecuencia nos encontraremos el problema del aire y el
oxígeno en situaciones de ejercicios de lápiz y papel. En el lenguaje coloquial
es común pensar que el aire y el oxígeno son la misma cosa, pero no lo es, el
aire es una mezcla de gases y el oxígeno es solo su segundo componente más
importante, de hecho, el aire está compuesto en su mayoría de nitrógeno
molecular. Así pues, podemos decir que el aire es una mezcla de varios gases,
donde los dos componentes más dominantes en el aire seco son 21% en volumen de
oxígeno y 78% en volumen de nitrógeno.
El oxígeno tiene una masa molar de 15,9994 g / mol y el nitrógeno tiene
una masa molar de 14,0067 g / mol. Dado que ambos elementos son diatómicos en
el aire: O2 y N2, la masa molar del gas oxígeno es de
aprox. 32 g / mol y la masa molar de nitrógeno gaseoso es de aprox. 28 g / mol.
Figura 7. Principales componentes del aire en porcentaje a
volumen.
Tabla 2. Principales componentes del aire seco y su relación con varias unidades de concentración.
La masa molar promedio del aire es igual a la suma de las
fracciones molares de cada gas multiplicada por la masa molar
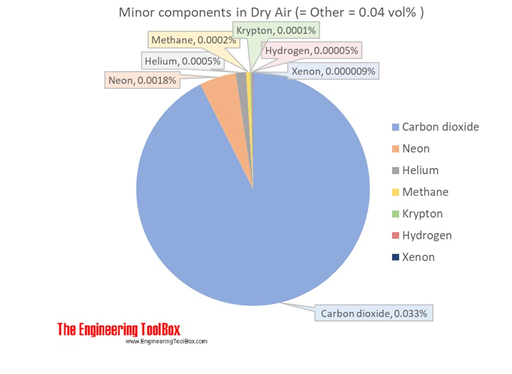
Figura 8. Componentes menores del aire.
La masa molar de aire seco con oxígeno, nitrógeno y los
demás componentes como se indica a continuación es 28,9647 g / mol.
















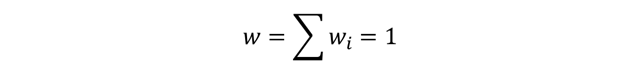
















No hay comentarios:
Publicar un comentario